Quadratic equations are an essential part of mathematics and form an integral component of the curriculum for universities and schools. Contrary to common perceptions of their actual utility the quadratic equations have a significant role to play across a range of fields, particularly for the field of research and development. The article below will delve deep into the quadratic equation 4x ^ 2 – 5x – 12 = 0 and explore its significance and concepts as well as methods to determine its origins. In addition, we will analyze the importance to these equations and their various uses.
What is the meaning of this Quadratic Equation?
A quadratic equation 4x ^ 2 – 5x – 12 = 0 is an inverse polynomial equation that is where the largest value of the variable (x in this instance) is multiplied by. This equation has been written with the formula ax2 + bx + c = 0. where a, B, and c are all constants. In our instance, the equation is a = 4 5, b = -5 and C = 12. The solution to this equation requires finding the values of x that meet the equation.
What is the Concept of Quadratic Equation: 4x ^ 2 – 5x – 12 = 0?
To comprehend the meaning of the quadratic equation to understand the concept of quadratic equation, we must to be aware of its basic structure and its properties. The most common format of the quadratic equation is:
2++=0ax2+bx+c=0
In this equation, a, b and c are constants. X is the variable. In our specific equation, 42-5-12=04×2-5x-12=0, the coefficients are a = 4, b = -5, and c = -12.
The roots or solutions of the quadratic equation which are indicated by 2×2 and 1×1 and 2×2, can be determined with the help of the formula for quadratics
=-+-2-42x=2a-b+-b2-4ac
Applying this formula to our equation, we can calculate the roots of 42-5-12=04×2-5x-12=0.

What are the Roots of this Equation?
To find the roots of the quadratic equation 42-5-12=04×2-5x-12=0, we can use the quadratic formula mentioned earlier:
=-+-2-42x=2a-b+-b2-4ac
For our equation for a = 4, b = -5 5, b = 5, and the c value is 12. After putting these numbers in, we find:
=5+-(-5)2-4(4)(-12)2(4)x=2(4)5+-(-5)2-4(4)(-12)
Further simplifying:
=5+-25+1928x=85+-25+192
=5+-2178x=85+-217
Therefore, the root of the equation 42-5-12=04×2-5x-12=0 can be found in:
1=5+2178×1=85+217
2=5-2178×2=85-217
Understanding the Roots
The quadratic roots of an equation offer valuable insight into the character of an equation and its representation in graphs. In the case of 42-5-12=04×2-5x-12=0, the roots are real and distinct since the discriminant 2-4b2-4ac is positive.
The discriminant D=2-4D=b2-4ac is used to determine the type of roots in a quadratic equation is composed of:
- If D>0D>0, then the roots are distinct and real.
- If D=0D=0, then the roots are real and the same (repeated).
- If D0D0, the root represent complex conjugates.
In our example, D=25+192=217D=25+192=217, which is positive, confirming that the roots are real and distinct. This information is essential in analyzing the graphic representation of the quadratic equation on an axis of coordinates.
Common Uses For Quadratic Equation
Although it is true that quadratic equations 4x ^ 2 – 5x – 12 = 0 may appear abstract to certain people, they have useful applications in a variety of areas. Here are some of the most common applications:
- Physics: Quadratic equations are frequent in physics, specifically in the field of problems that are related to motion. The equations define the path of projectiles as well as the movement of objects subject to gravity.
- Engineering Engineers utilize quadratic equations in a variety of applications, including electrical circuits, structural analysis and optimization issues. The equations assist in analyzing and tackling real-world engineering problems.
- Economic: Quadratic equations are used in economic modeling to study demand and supply graphs, profits maximization along with cost-functions. They offer valuable insight into the behaviour that economic system.
- Computer Science: algorithms and computational techniques typically require the solution of quadratic equations. This is particularly the case in computer graphics in which quadratic equations describe curves and forms.
- Biology: Quadratic equations can be utilized in biology to simulate the growth and decline of populations. The equations aid biologists in analyzing the evolution of populations throughout time.
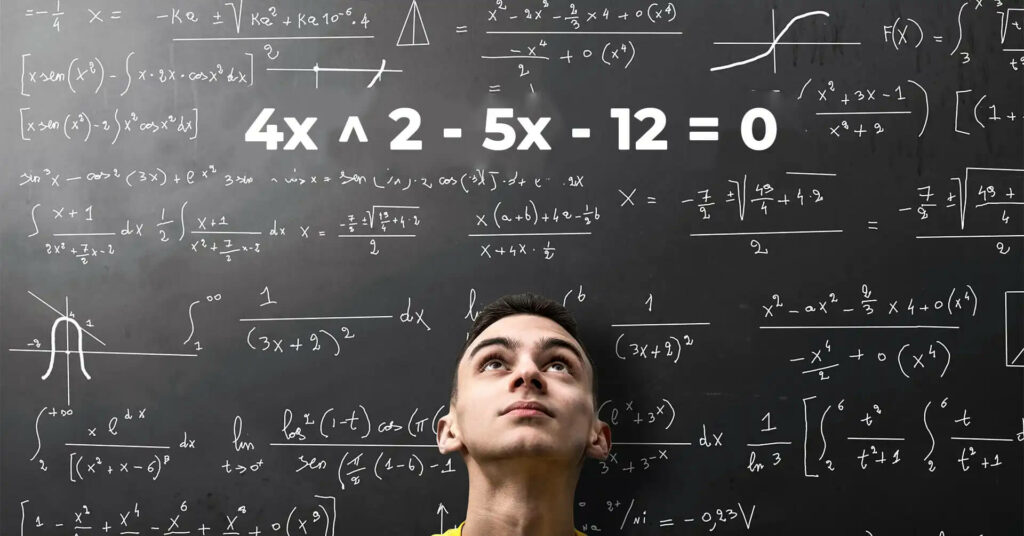
To conclude
In the end that quadratic equation 42-5-12=04×2-5x-12=0 is an opening to understanding the larger notions that are inherent in quadratic equations. Understanding its significance, implementing ways, and studying the root causes not only improves our mathematical skills but also gives us useful techniques for solving real-world problems. Check more on AOIME.
Quadratic equations 4x ^ 2 – 5x – 12 = 0 Despite their abstract nature, can be found in many applications across a variety of disciplines. From engineering and physics to computers and economics The principles of quadratic equations play an important role in analyzing and solving difficult problems. Understanding the importance of quadratic equations opens the way to an knowledge of mathematical concepts that regulate our lives.










